The pentagons on opposite sides of a regular dodecahedron are in opposite orientations, in the sense that if you duplicate the dodecahedron without rotating it, and stack the copy on the original, the two touching pentagons will be “perfectly misaligned”.
The symmetry of a regular dodecahedron includes reflections. In particular, it includes the central inversion, which is equivalent to three coordinate sign changes or to three orthogonal mirrors.
The snub dodecahedron has only the rotation symmetries of a regular dodecahedron, with no reflection symmetries. It is as if we took the pentagonal faces of the dodecahedron, separated them all slightly, and twisted them all uniformly around their centers. How does this preserve the 2-fold rotations of the symmetry? The figure below attempts to illustrate this. Use your mouse or touch interface to rotate the view in a way that keeps the red axis vertical, and rotate it 180 degrees.
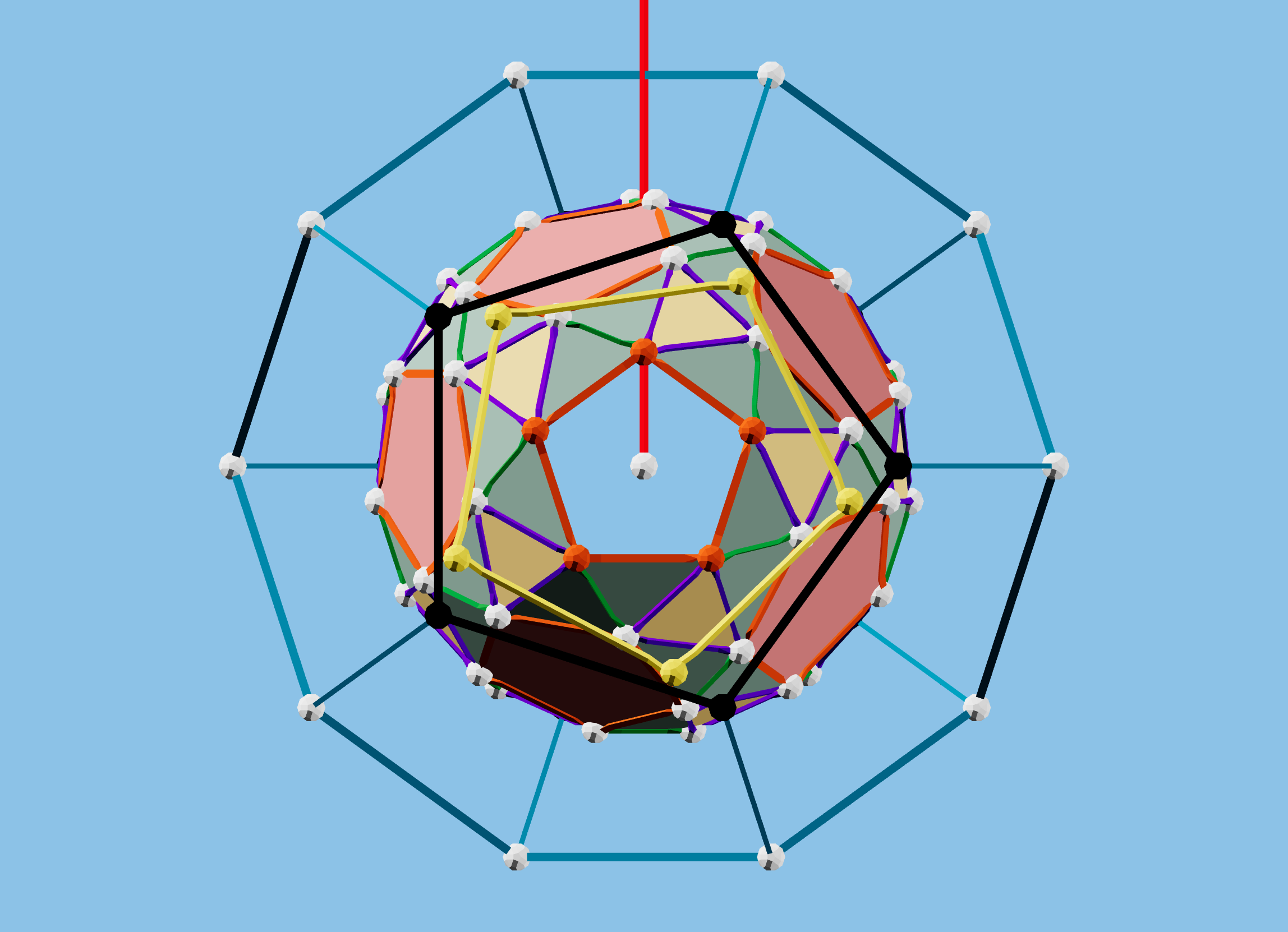
The black pentagons of a regular dodecahedron do exactly what we expect; think of one vertex as the tip of an arrow, and you can rotate that pentagon in the direction of the arrow until it swings around to the back.
What’s harder to see is that the same rotation preserves the twist of the yellow pentagons! These pentagons are not exactly those of a snub dodecahedron, the Archimedean solid, but any twist applied to all 12 pentagons works the same way.
The fun case is another special case, illustrated by the orange pentagons. That polyhedron is again a topological cousin of the snub dodecahedron, but slightly different. In this case, the pentagon twist is just right so that the rotation around to the back just pivots the pentagon around one vertex! This gives us the beautiful pentagonal prism tunnel straight through the object… and there are six of them in a symmetric arrangement! This defies intuition, no matter how many times I see it.