With vZome and Zometool, it is fun to look at 3-dimensional “shadows” of higher-dimensional figures. However, these shadows become hard to understand unless we use hidden surface removal, a technique well-known in computer graphics.
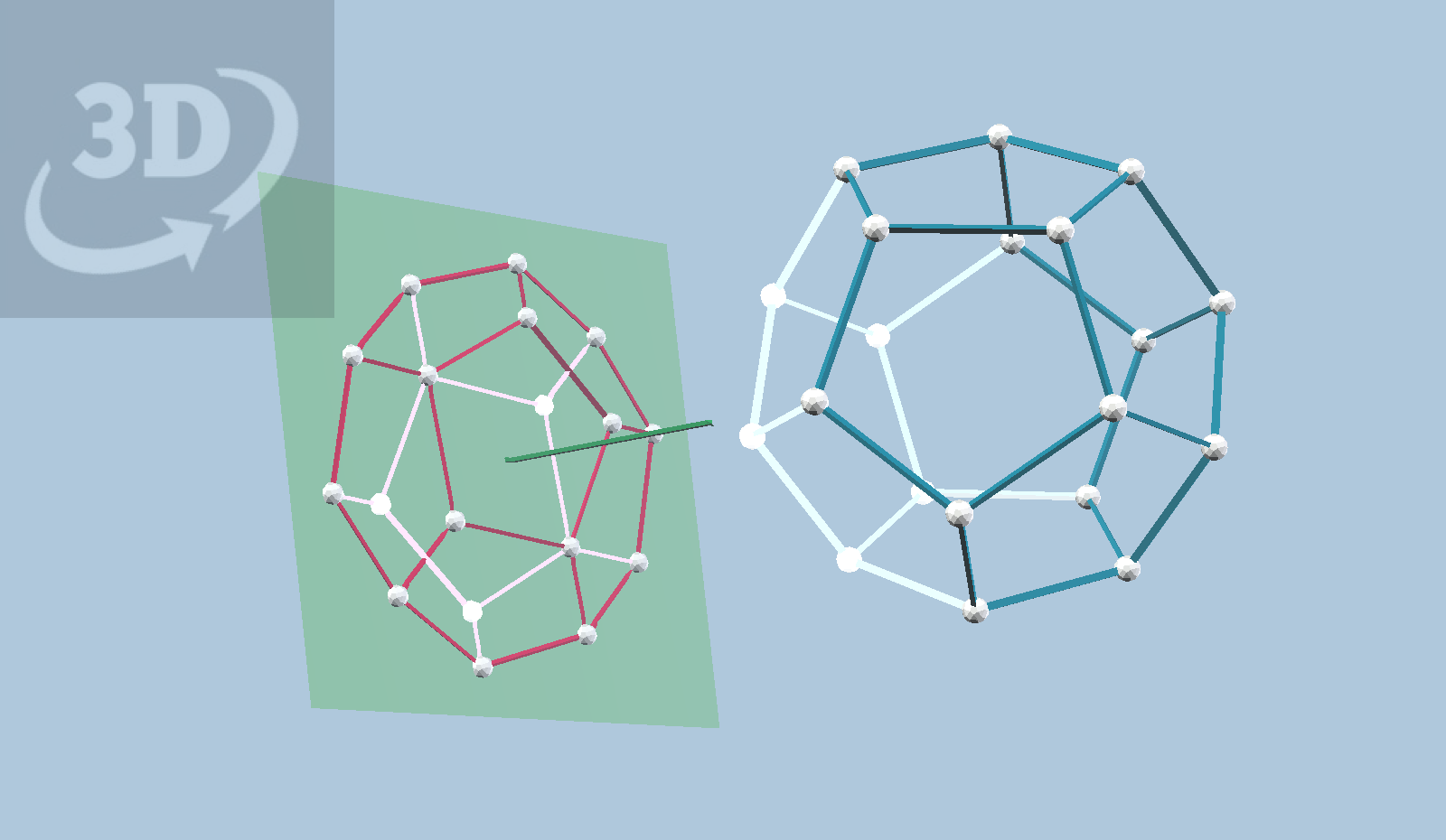
This is illustrated in the figure above, showing a wire-frame dodecahedron projected to a plane, as if the sun (in the direction of the green line) were casting a shadow. In the first scene, all the edges of the dodecahedron are shown, and it is a little hard for our brains to see this as a dodecahedron. In the second scene, we have removed the edges of the “back-facing” pentagon faces, considering the “front” as the side in the sunshine. We could just as easily reverse our notions of front and back. Either way, this shadow is much easier to see as a dodecahedron!
Notice that there are a number of edges that form the boundary of the projection. We never want to remove those!
This gets much more important when we start projecting 4-D shapes to 3-D. Below we see two projections of the hypercube. The blue lines are projected from the “back” of the hypercube, and it is difficult for us to find the projected cubes (now rhomboids) in that view. If we show only the red edges (from the “front”), we can more easily see those projected cubes clustered around the center.
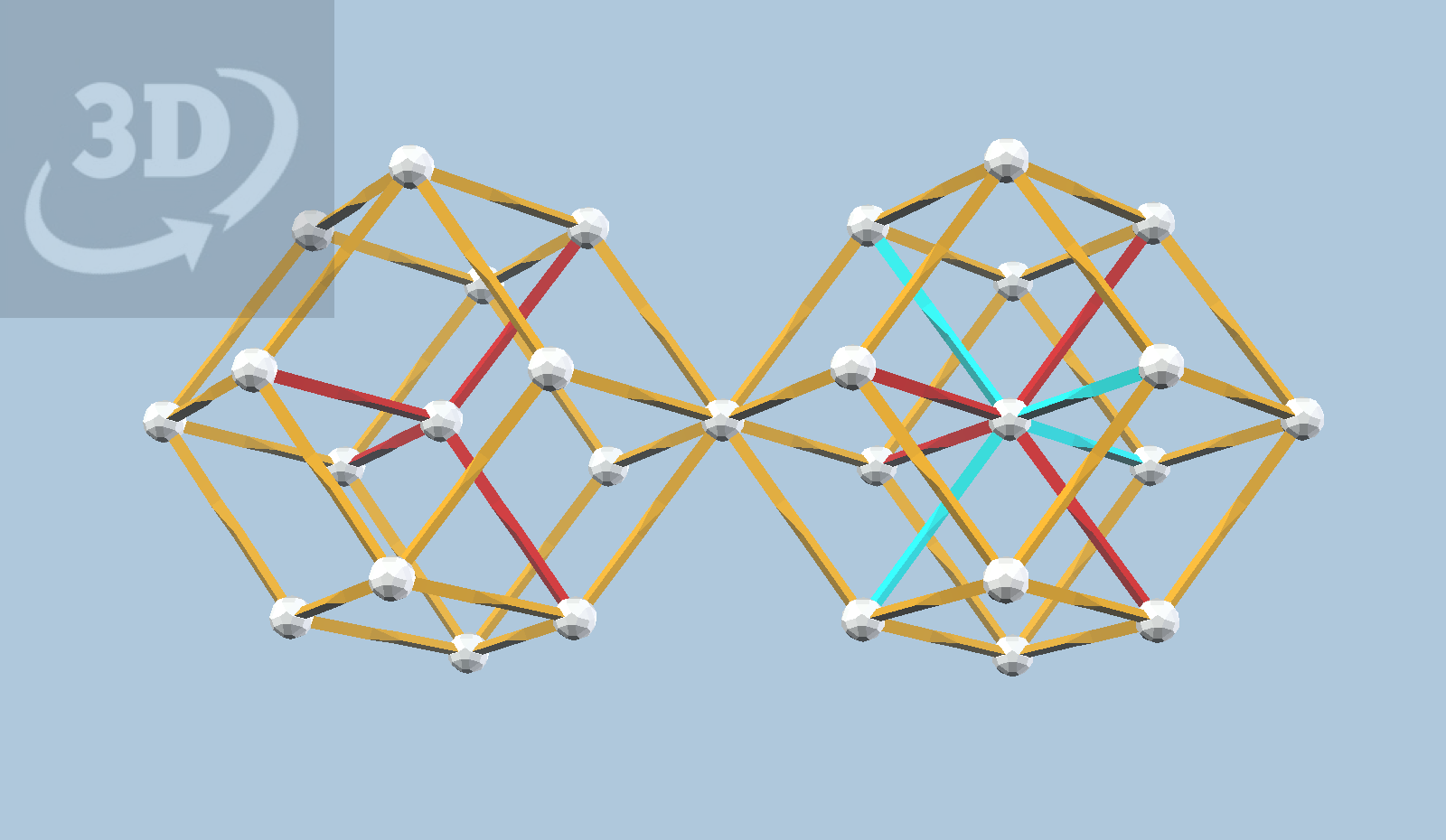
Even here, if you don’t rotate the view in the figure above, your brain will have difficulty seeing the 3-D shapes. This is because your eyes are again projecting 3-D to 2-D, just as in the original example, and here we cannot hide the back faces without destroying our understanding of the 3-D structure, which is crucial to getting insights about the 4-D structure!
As we look to higher-dimensional objects, this problem gets worse and worse. Without hidden surface removal, the 10-cube projection below is simply impenetrable.
