A simplex is a shape analogous to an equilateral triangle in 2D, or the regular tetrahedron in 3D. The 4D simplex is called the 5-cell, since it has five cells that are regular tetrahedra. The symmetry group of the 5-cell is A4, a Coxeter reflection group. That group admits the possibility of nine distinct uniform polytopes, including the 5-cell and two relatives shown below.

The first scene above shows a very special 3D projection of the Runcinated 5-cell, one that uses Zometool struts and has ghost symmetry. This means is retains some of the five-fold symmetry of the 4D polytope, visible only from one of two specific directions.
The last four scenes above show the four possible oblique projections of the polytope that result in the projection being stretched out in the yellow direction, just enough that most of the edges can still be represented with blue and green Zometool struts.
These oblique projections to 3D are parallel projections, but projecting to a hyperplane (a 3D space) NOT perpendicular to the line of projection. The figure below shows such a projection, this time of the omni-truncated 5-cell, the largest in the family. It further shows an oblique projection to a 2D plane. Notice that the red plane is not perpendicular to the line of projection.
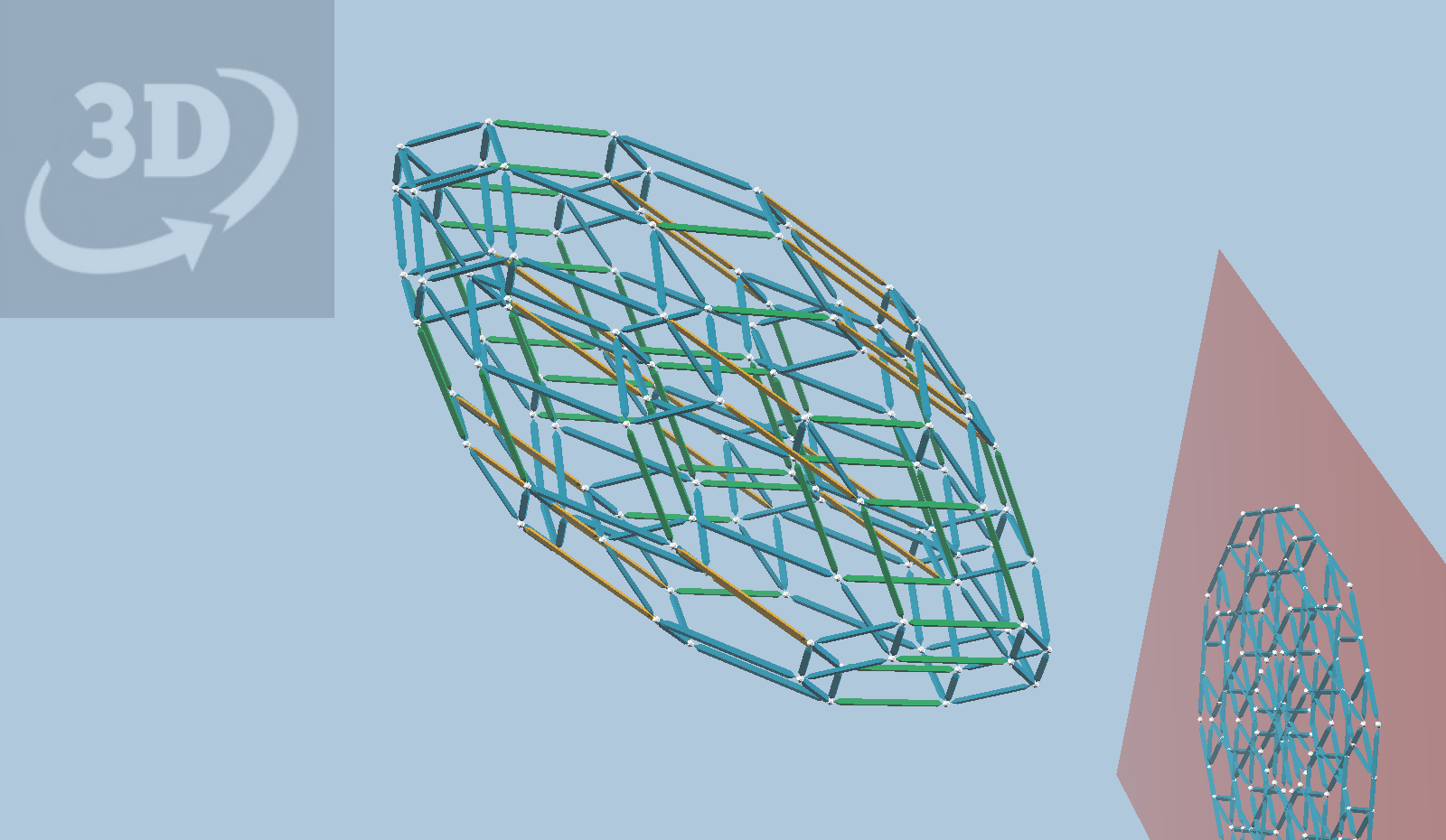
The remarkable thing here is that the five-fold symmetry of the original polytopes are subtly preserved in the 3D projections, recoverable only by projecting further to 2D. Furthermore, a judicious choice of 2D plane for an oblique projection can even recover the perfect, circular five-fold symmetry.