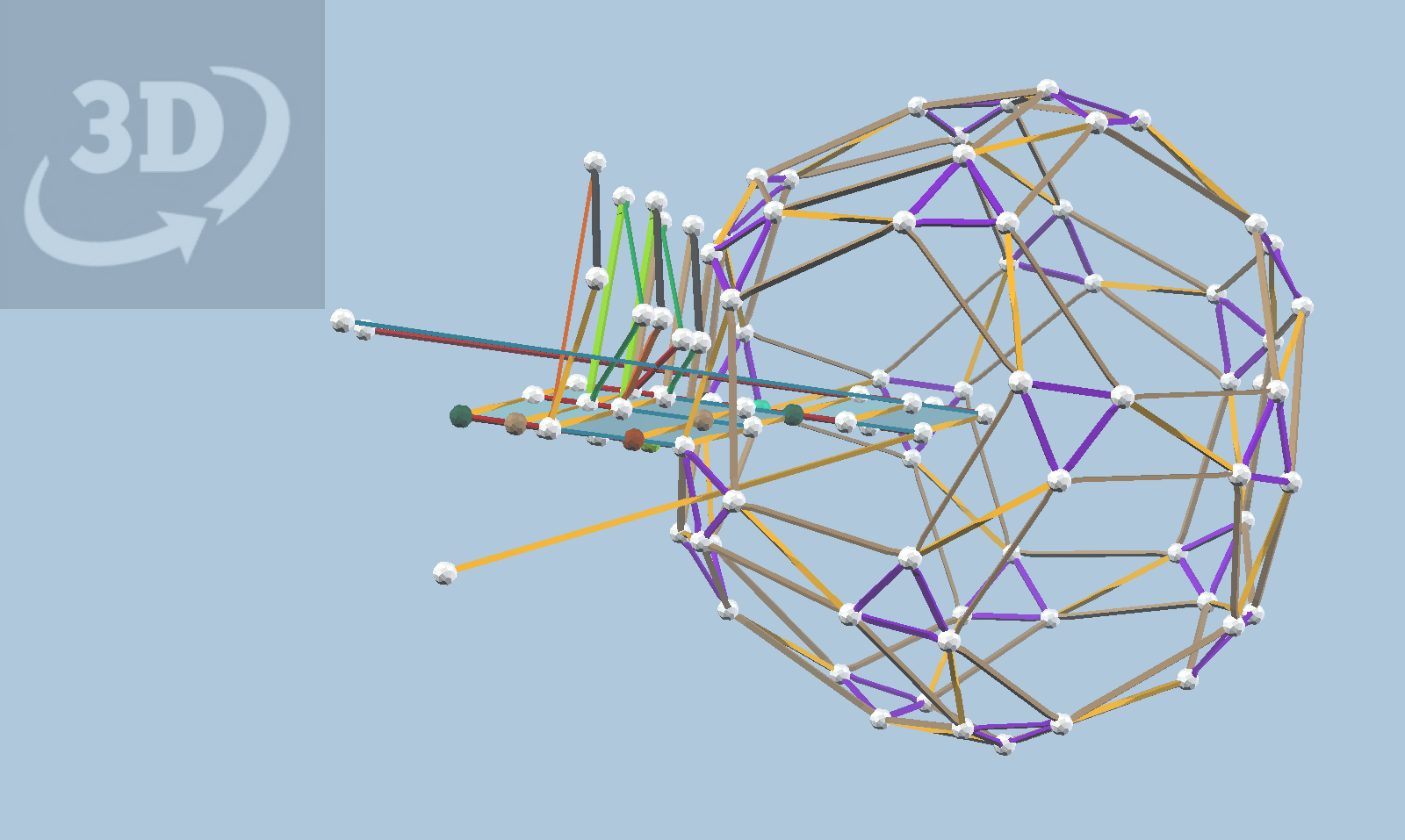
The great rhombicosidodecahedron is an Archimedean solid constructible with Zometool in three sizes. There are 24 other variations of this shape that can be constructed, using the three sizes of Zometool struts, if we are willing to give up uniform edge lengths.
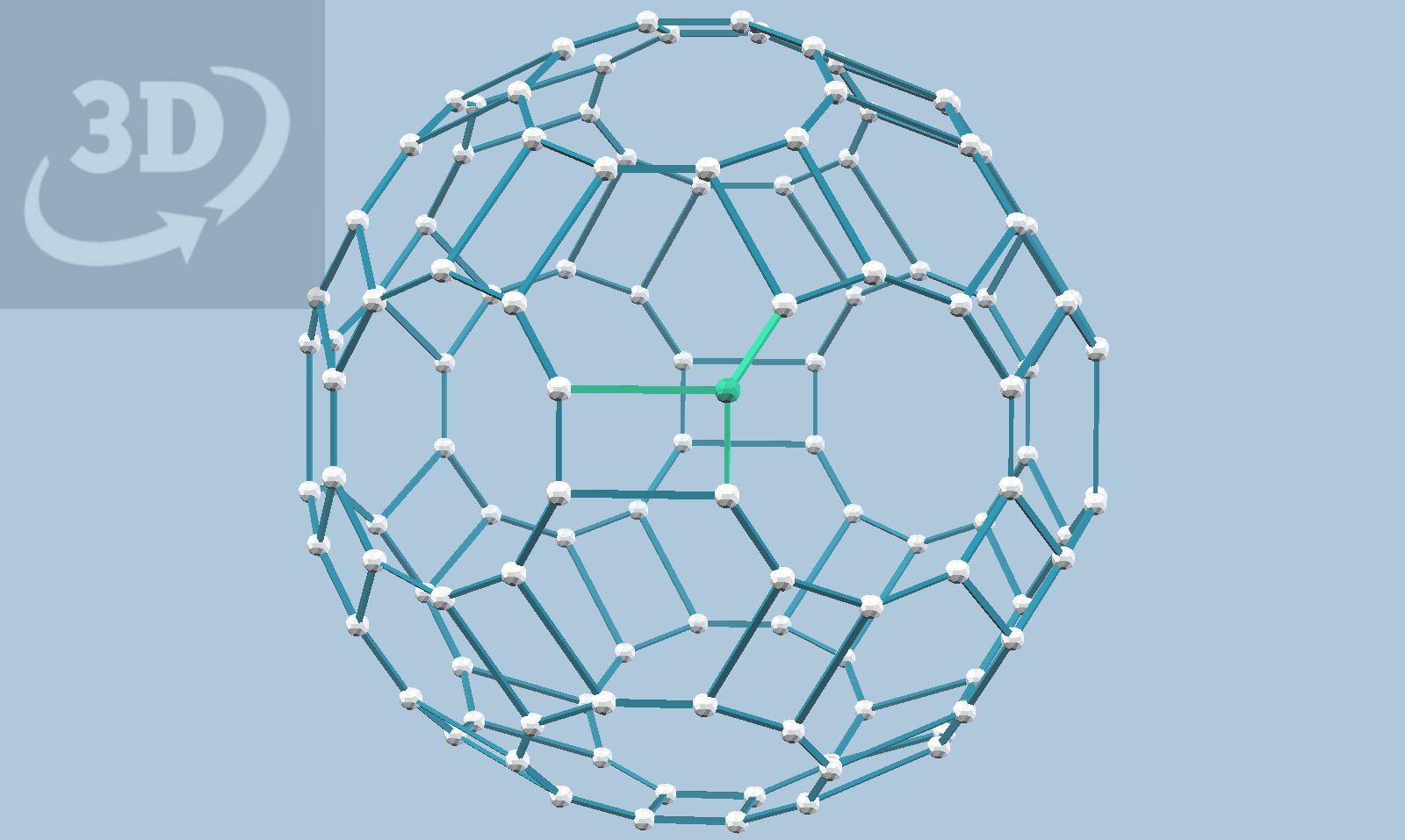
The total number of variants is then 27. This makes sense because there are three distinct orbits of edges under icosahedral symmetry, and for each orbit there are three choices for the strut length. Nathaniel Lindell introduced me to these ideas, and in fact he has produced an Observable notebook illustrating the relationship between the vertices of these polyhedra and the icosahedral symmetry group. In his notebook, there are 19 orbits in the interior of the fundamental region. I was puzzled by this until I realized that some orbits represent more than one variant. For example, the variant made with 180 b0 struts uses the same vertex orbit as the one made with 180 b1 or b2 struts.
The 19 orbits are arranged in a kind of odd hexagon in Nathaniel’s notebook, which naturally renders them on the surface of a sphere. The hexagon makes perfect sense once you realize you are looking at three faces of a 3x3x3 parallelipiped.

Some of the vertex balls are colored to correspond to predefined strut orbits in vZome, as in the Observable notebook mentioned earlier.
You can download this model and open it with vZome, then apply icosahedral symmetry and central symmetry to a particular vertex and its association edges, to obtain the corresponding variant of the great rhombicosidodecahedron.
If you select just the vertex, not the adjacent edges, and apply just the icosahedral symmetry without the central symmetry, you get the vertices of a variant of the snub dodecahedron. You can use the convex hull command to add the edges, while the vertices are still selected. The regular snub dodecahedron is not constructible with Zometool, not even its vertices, but you can immediately see that we have 19 colorful alternatives, some very close to regular.