Can the vertices of a shape like this lie exactly on a sphere? By “like this”, I mean with the implied symmetries and planar faces.
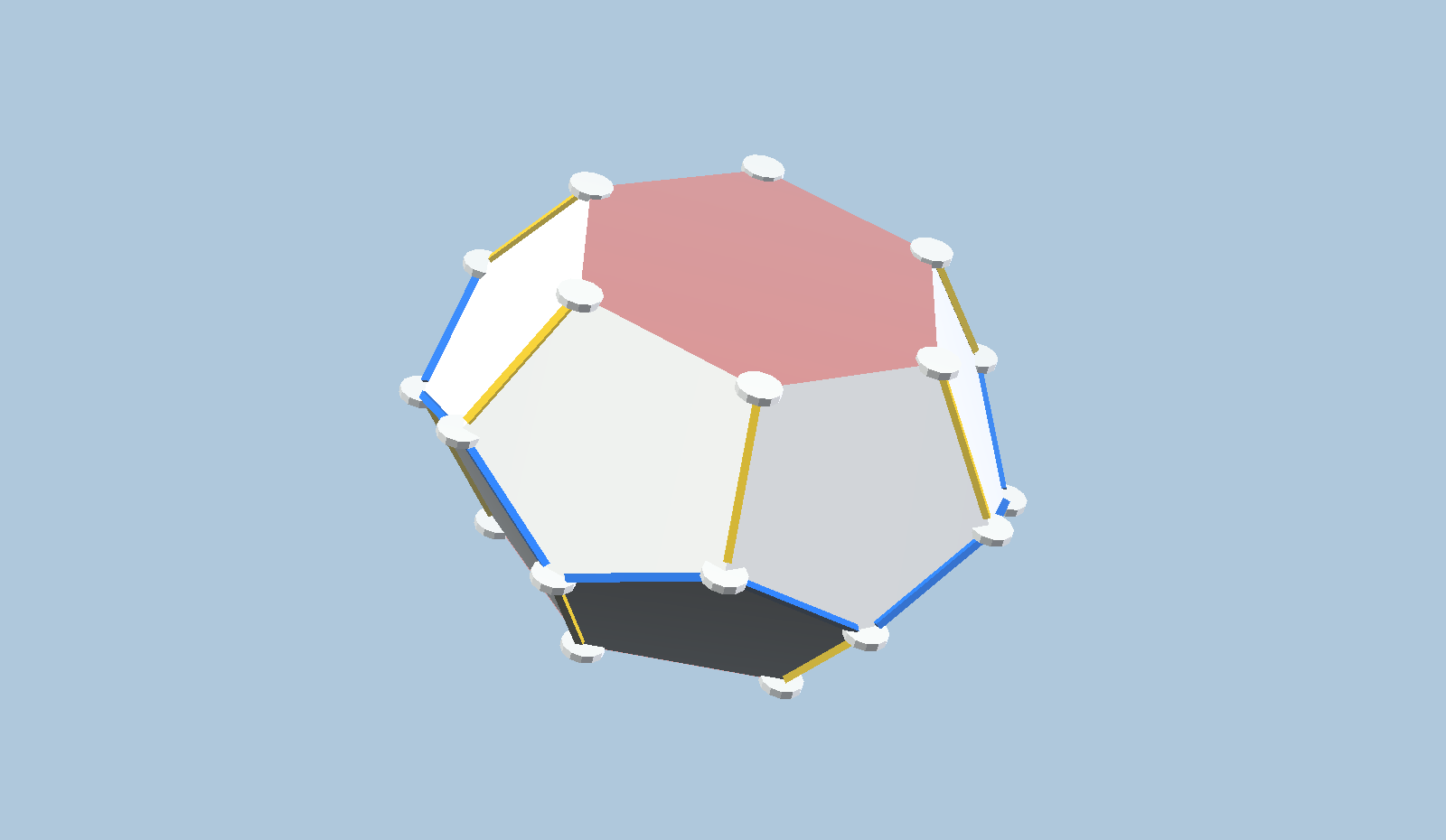
It is not too hard to show that there must be such a shape that can be inscribed in a perfect sphere. Consider that the shape above is a truncated version of this shape:
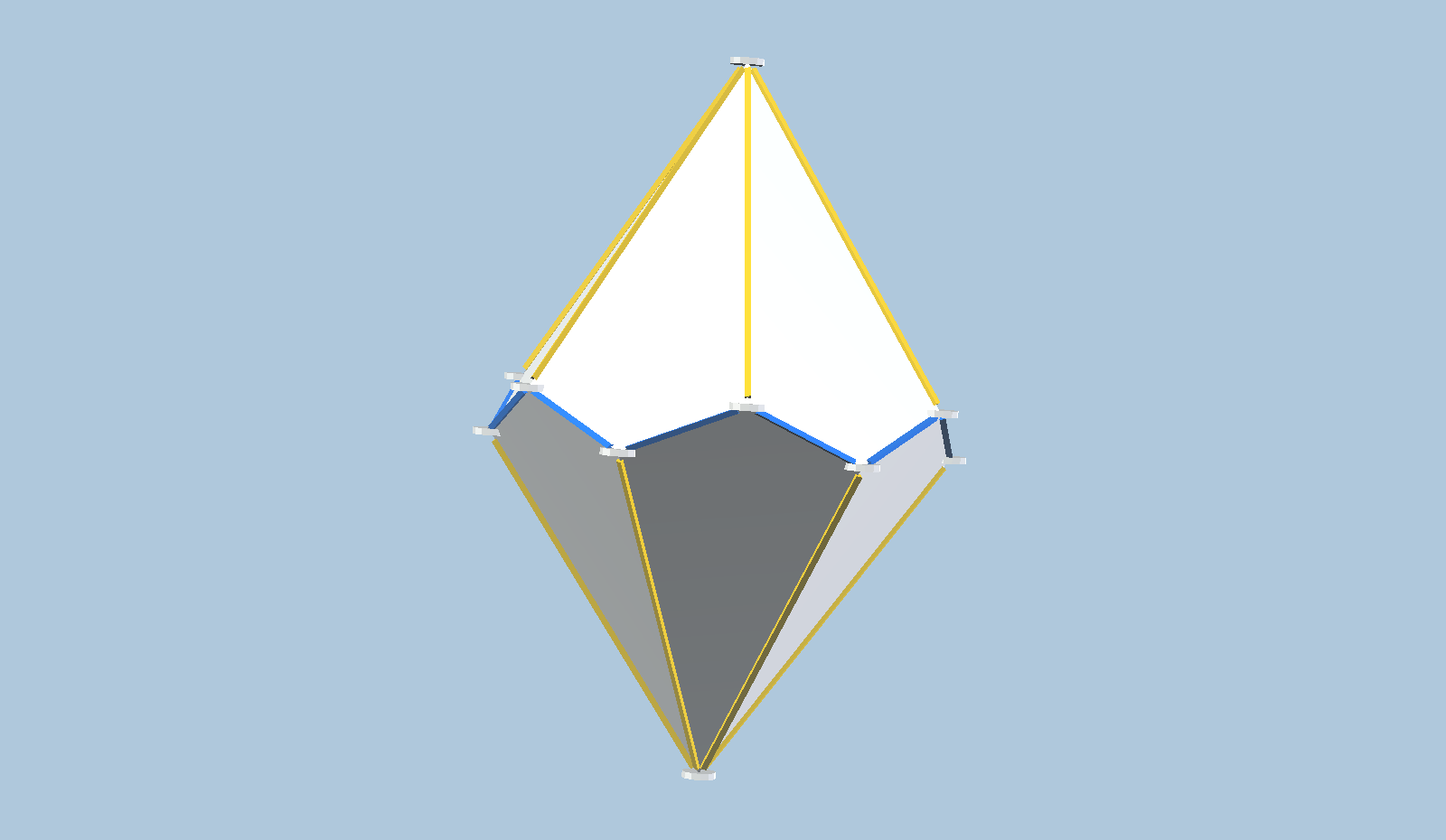
The blue edges zig-zag between two sets of vertices, lying in two parallel planes. The center of the shape lies midway between those planes. The distance from those 12 vertices to the central plane was chosen arbitrarily, and the rest of the figure is then determined by symmetry and planarity. In other words, we have a 1-parameter system, and we can call that distance parameter D.
We can reduce D closer to zero, and the generated yellow edges will get shorter and shorter, meeting at the center of the object in the limit, as the overall shape approaches a disk. We can also increase the zig-zag distance, and in the limit the yellow edges will get infinitely long, as the overal shape approaches an infinite cylinder.
Unless we’re at one of those limits, the blue zig-zag clearly defines two parallel circles, and those circles necessarily define a sphere uniquely. The radius of that sphere cannot get arbitrarily small, so there must be a lower bound of D at which our two points (where the yellow edges meet) exactly touch the sphere.
Similarly, as D grows large, the two points recede toward infinity, but the sphere approaches diameter 2D. Clearly the yellow line segments must always penetrate the sphere in 12 points.