vZome offers several of these topological equivalents to the snub dodecahedron. Here are some I haven’t seen before. I discovered them while exploring the icosahedral orbits in Observable. Orbit cylinders in that visualization turn out to be excellent predictors of snub dodecahedra constructible with vZome orbits, such as these designs.
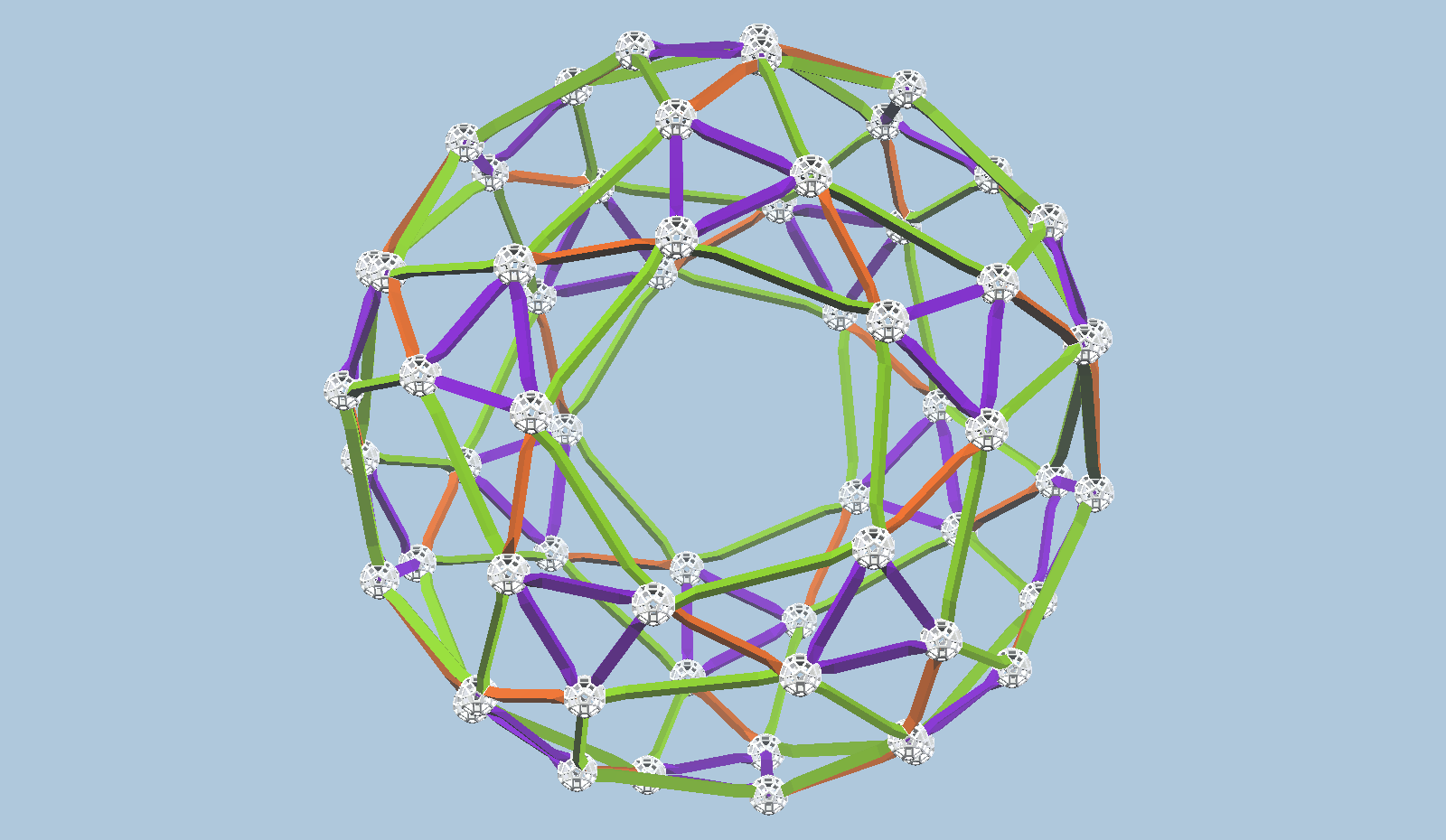
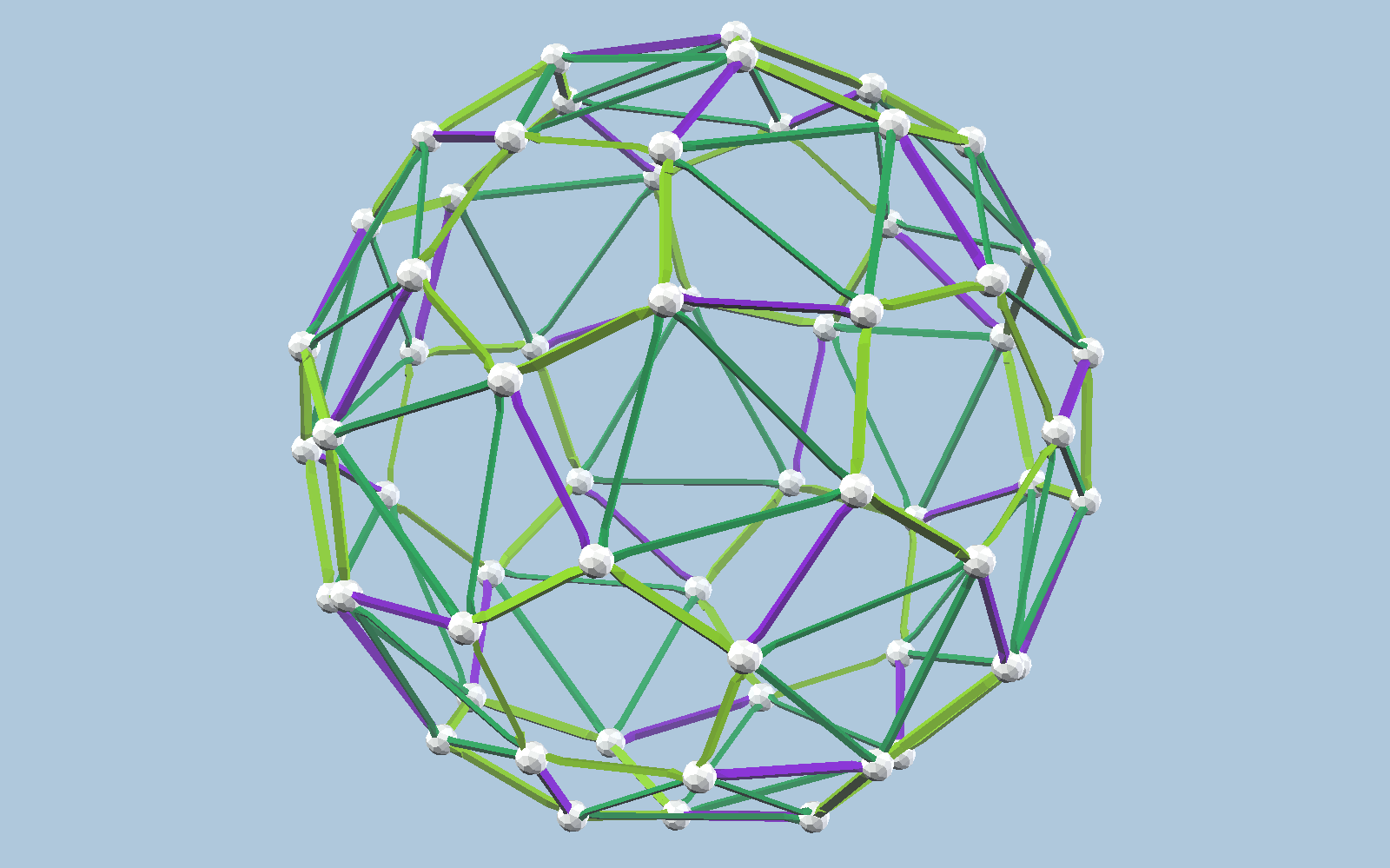
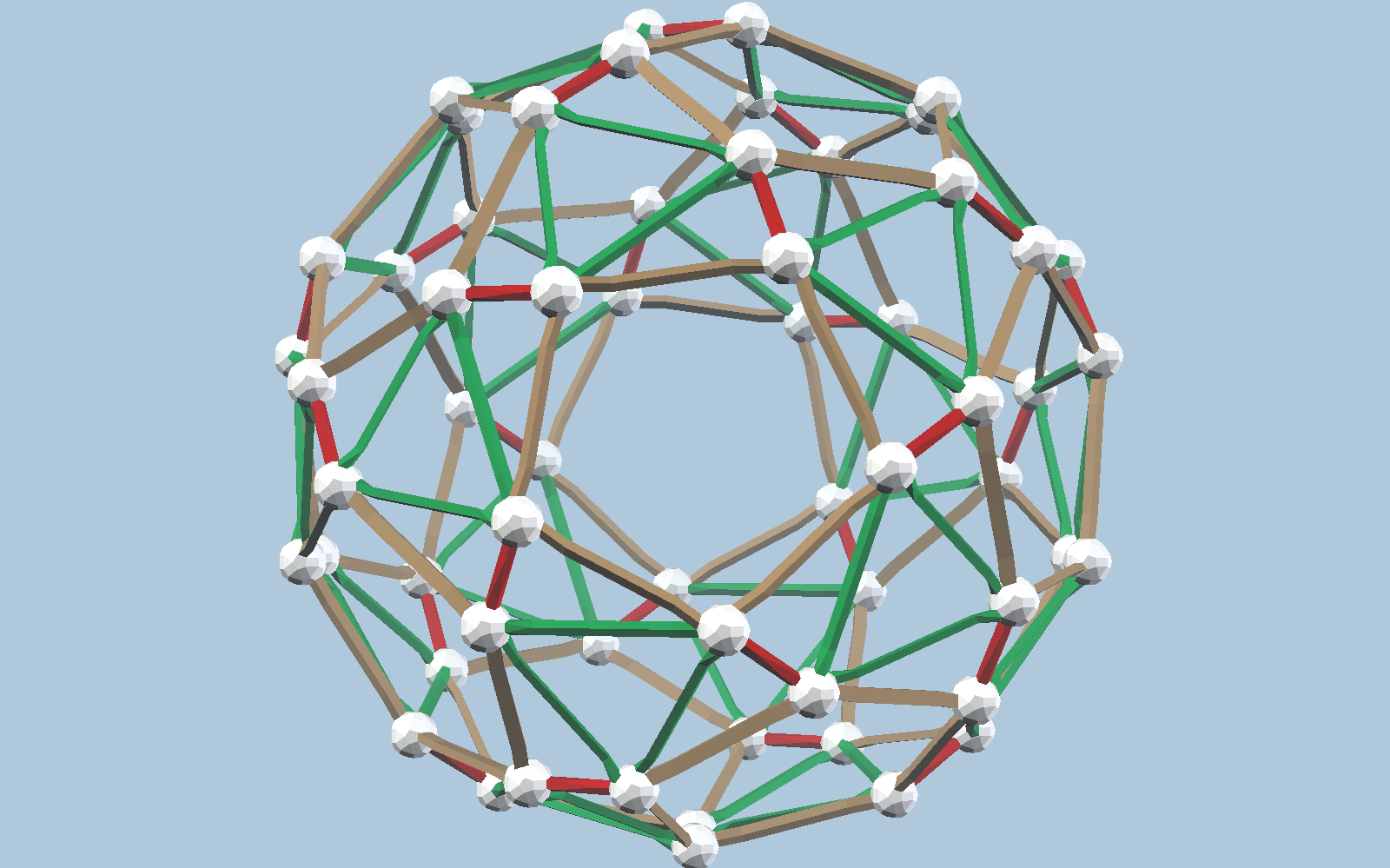
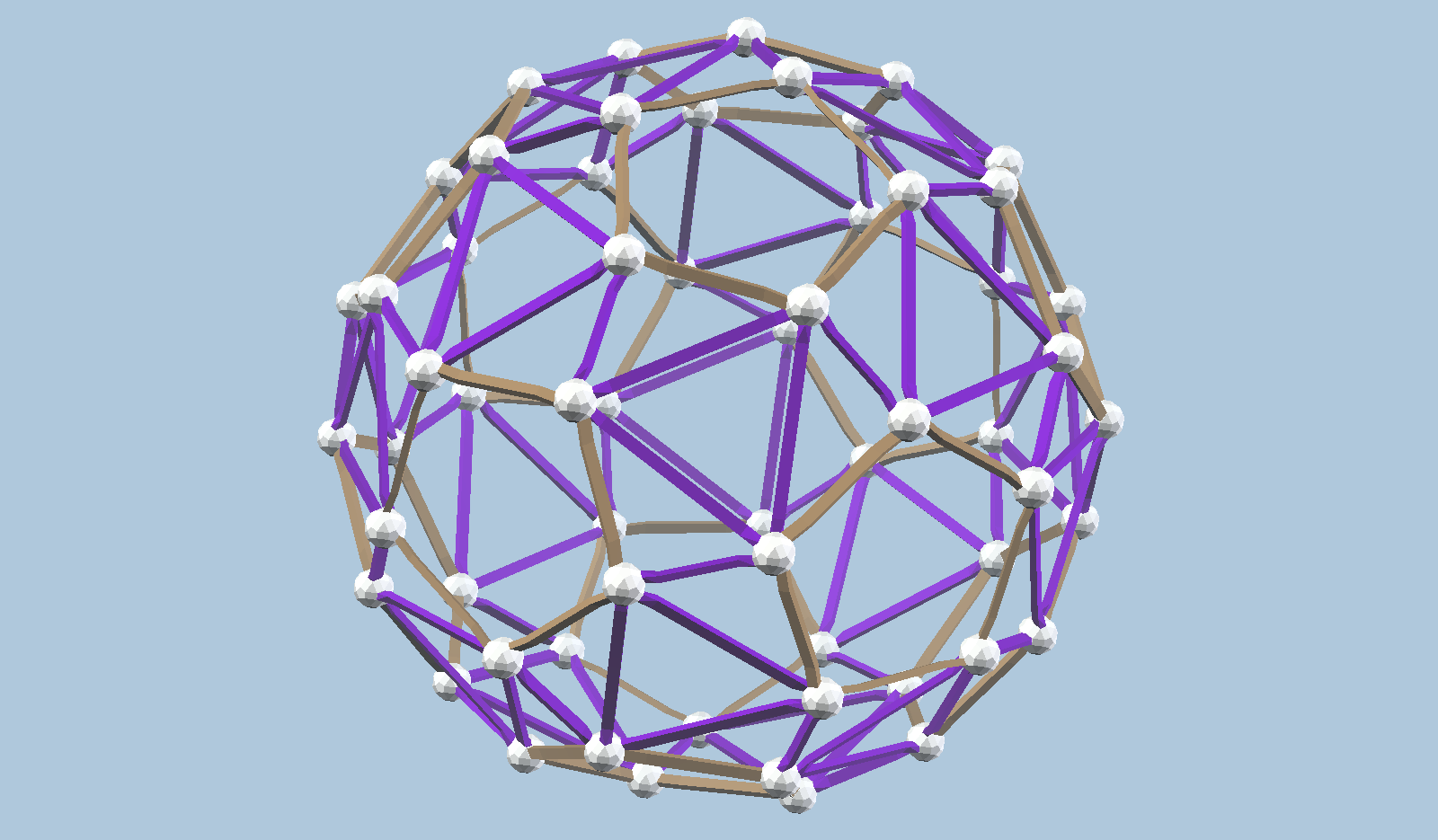
Download the vZome file for any of these, open it with the vZome desktop app, and you can use the “undo” command repeatedly to see how I constructed the necessary vertices, looking for points on the sphere where several orbit planes of different colors intersect. Another way to see this is to visit vZome Online and load the vZome file there; the command history is actually visible and randomly accessible if you do that.
In all cases, the result is most naturally understood as the alternating vertices of some variant of the great rhombicosidodecahedron, whose edges will always be blue, and whose faces always have an even number of sides. Notice that the vertices of these blue polyhedra can be colored black and white in an alternating fashion, so that a white ball is only connected to black balls, and vice versa. This means that each of the structures above exist in two forms, one “right-handed” using white balls and one “left-handed” using black balls. We say they are chiral forms.
