Whence Orange Struts?

Where do orange struts come from in vZome? This article answers the question in some depth.

The interactive 3D viewer below shows a golden rectangle with blue edges and red diagonals. This is easy to construct with Zometool. The other golden rectangle however, the one with orange diagonals, is equally constructible with blue Zometool struts, but you cannot construct the diagonals because they are no longer red struts.

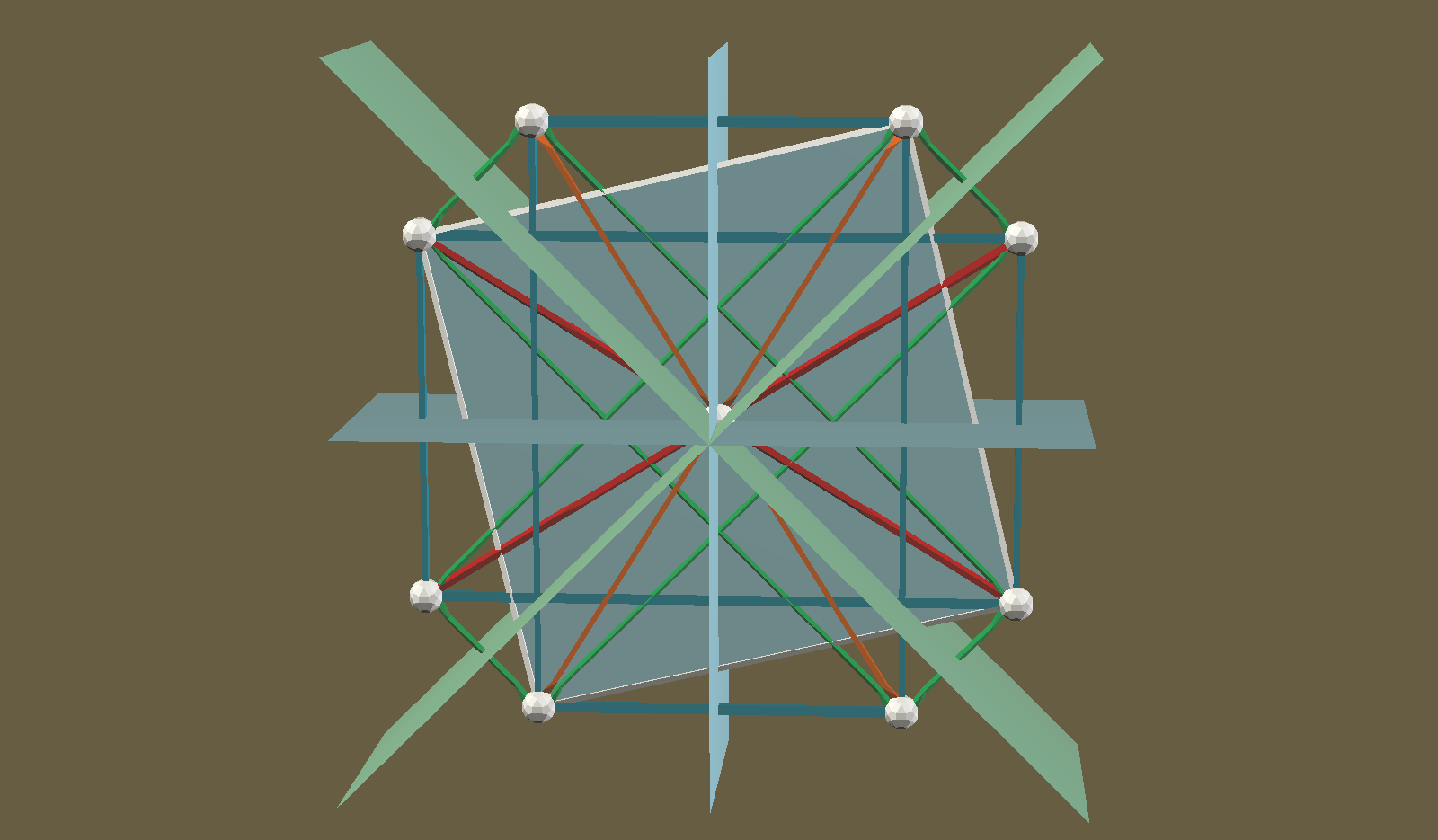
Ignoring the blue square for a moment, consider the two blue mirror planes. These are two of the fifteen blue mirror planes that are the defining characteristic of the icosahedral symmetry in Zometool. These two mirrors reflect both of our golden rectangles, preserving the reflection symmetry of each rectangle.

However, notice that we need a green mirror plane if we want to reflect the red-diagonal rectangle into the orange-diagonal rectangle. Green mirrors are not part of icosahedral symmetry; they are a part of octahedral symmetry, where they are required to support four-fold rotations. Icosahedral and octahedral symmetry are two distinct 3D reflection groups, and importantly, neither is a subgroup of the other, though they do share quite a few subgroups.

Orange lines were first defined by Fabien Vienne, a gifted architect and one of the inventors of green Zometool struts. He didn’t think of them as orange, however; he called them “rouge symmetrique” (symmetric red), because they have the same length as red struts, and he felt they “completed” the Zometool system to support octahedral symmetry. This is partly true, in that they let you build Zometool models that have octahedral symmetry. However, Fabien’s struts, like my orange struts, necessarily had a different shape than red struts, and fit into different holes in the Zome ball. This is a manifestation of the fact I mentioned above; we have to choose whether our Zome balls and struts will be shaped according to icosahedral symmetry or according to octahedral symmetry. We cannot have both.