The 4-dimensional 120-cell or hyperdodecahedron, projected obliquely to 3-D.
The 120-cell is a 4-dimensional polytope, containing regular 3-D dodecahedral cells, arranged three around an edge and four around a vertex. In our 3-D world, we cannot do that with regular dodecahedra, but it is possible in 4-D mathematical space.
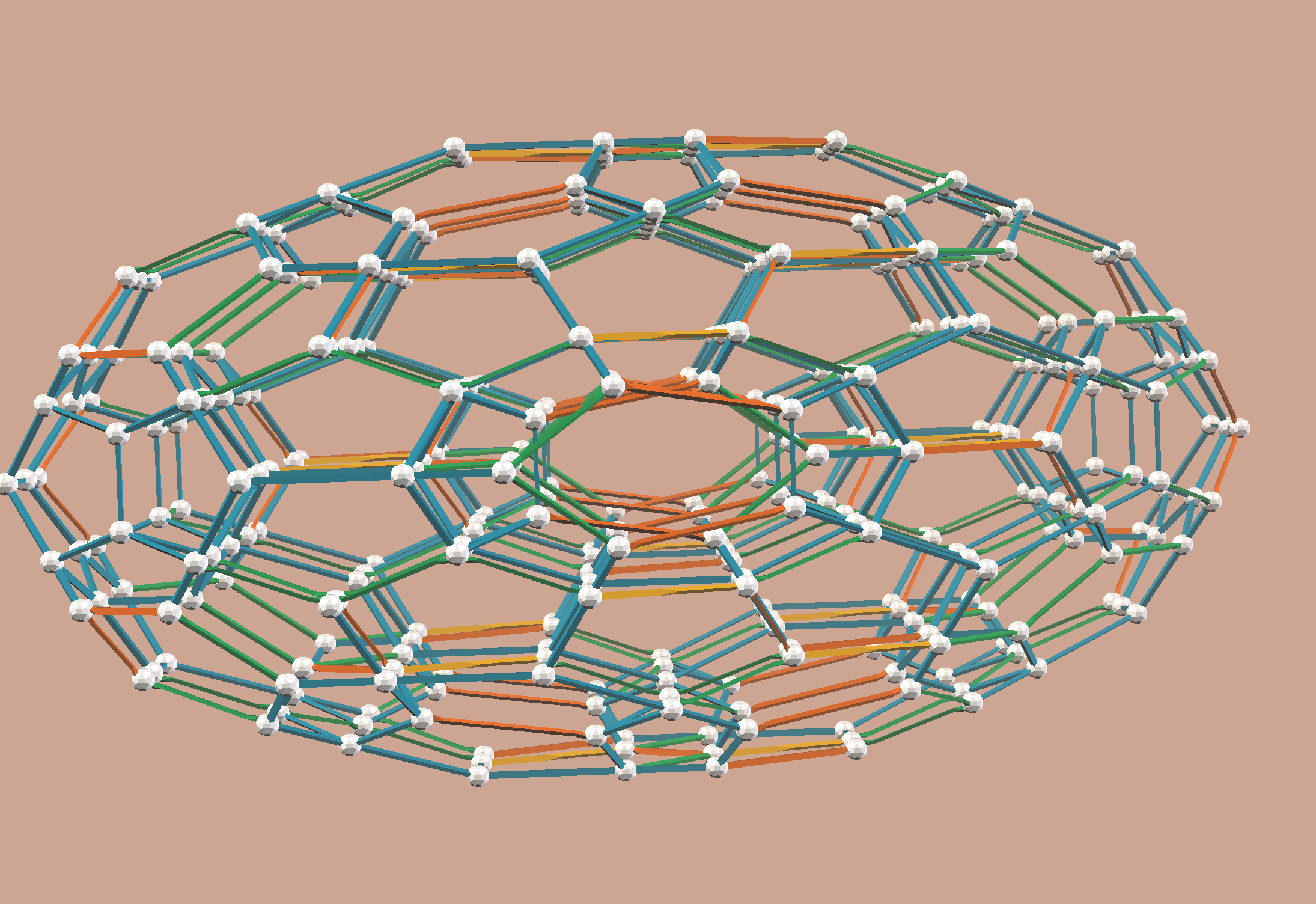
We cannot see 4-D objects unless we make a 3-D “shadow”, as if a light source in the 4-D world shone through the objects onto a 3-D hyperplane, analogous to how shadows in our 3-D world are cast onto 2-D planes. If the light source is very far away (like our sun), we get a parallel projection, with no foreshortening since there is no useful notion of “nearer to” or “farther from” the light source. If the projection plane (or hyperplane, in this case) is at right angles to the direction to the light source, we get an orthogonal projection. If we tilt the projection plane a bit, we get an oblique projection, like your elongated or shortened shadow on a sidewalk whenever the sun is not directly overhead. (Fun thought experiment: when is your shadow the same length as your height?)
This design is just that, an oblique parallel projection of the regular 120-cell into 3-D space. The angle of projection is very particular, and it yields an object that has been stretched out along a yellow Zome strut line. This is a nice projection because it is almost constructible with regular Zometool pieces – blue, green, and yellow struts are all real. The orange struts, however, are only available as 3-D printed parts available from Shapeways. These orange struts are commonly seen in vZome.
The projection is essentially defined such that the final object still has regular dodecahedra made from blue Zome struts… just not in the center, as you’d normally see with the usual Zome projection of the 120-cell.