I've been learning about the E_6, E_7, and E_8 lattices lately, with a lot of help from David Richter. If one reads about these in Coxeter's "Regular Polytopes", one comes across the Gosset polytopes. It is well-known that the 8-dimensional Gosset polytope, 4_21, has 240 vertices, corresponding to the vertices of two concentric 600-cells. David showed me how to compute the edges of 4_21 by finding all pairs of those 240 vertices that have a dot-product of one. This turned out to be pretty trivial to "code up" based on vZome and my existing 600cell.vef dataset, and the result is what you see below.
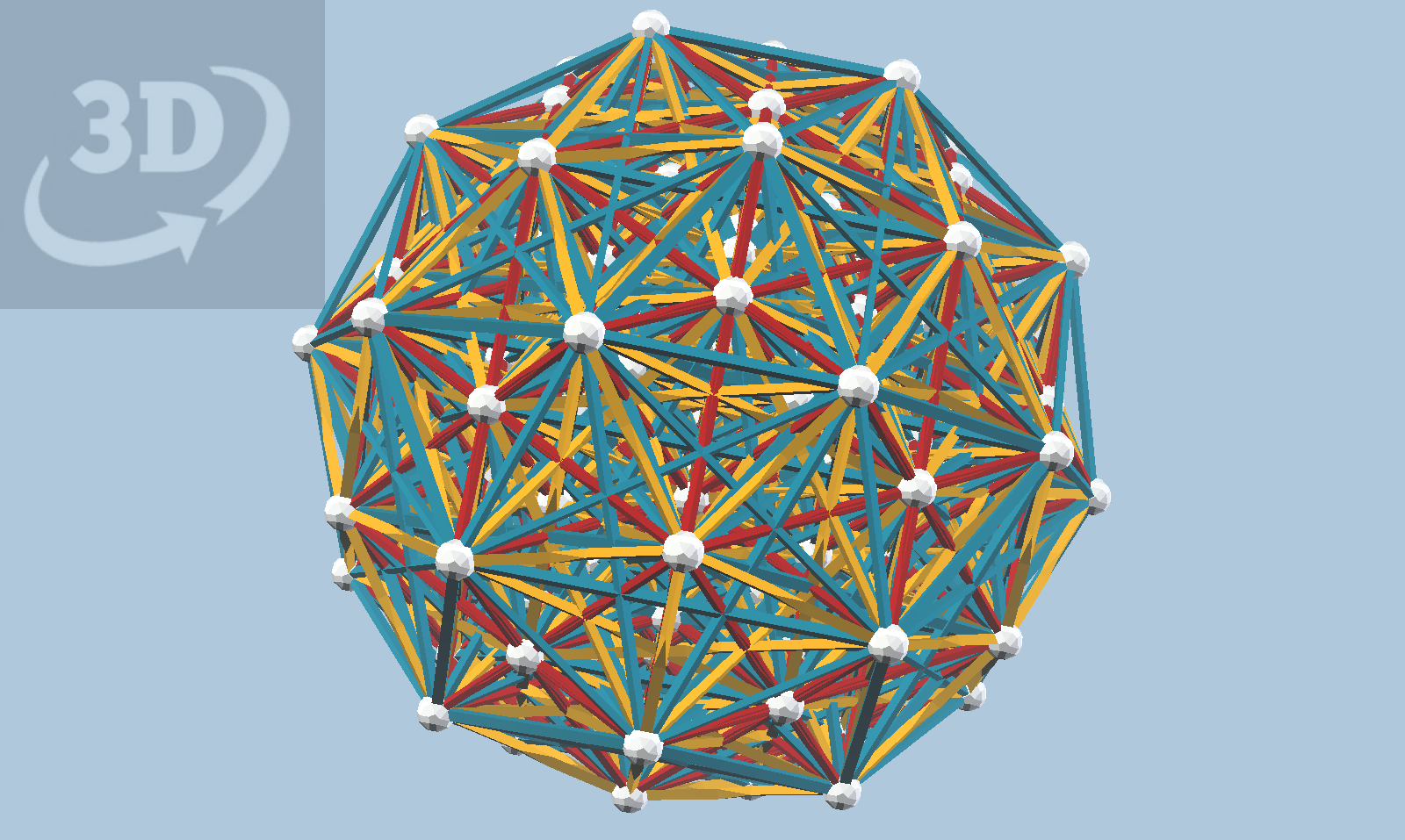
It definitely appears that David's conjecture he stated in Banff may well be correct: that this projection of 4_21 can be constructed by building two concentric 600-cells, scaled by the golden ratio, then connecting any two balls when you can with a red, yellow, or blue strut. The model is quite clearly heavily interconnected, with every strut intersecting several others in the interior. This is the effect of projecting 6720 edges (between 240 vertices) from eight dimensions down to three... there are no edge intersections in the 8-dimensional original.
Although it might be difficult to prove, I suspect that the projection of 4_21 into 4-dimensional space has H_4 symmetry. It is certainly true that the E_8 reflection group contains a subgroup isomorphic to the H_4 reflection group, a fact we will explore this weekend in the Chicago Zomeposium hosted by Chris Palmer.
David also told me how to compute the vertex figure of 4_21, which turns out to be 3_21, the Gosset polytope in seven dimensions. Where 4_21 has E_8 symmetry, 3_21 has E_7 symmetry. To find a single 3_21 in a 4_21, select any vertex of 4_21, then find the nearest 56 vertices, and all (756) "short" edges among them. This turns out to be another trivial exercise in finding vertex pairs with dot product equal to one. The result of this exercise, after centering on the origin, is shown below.
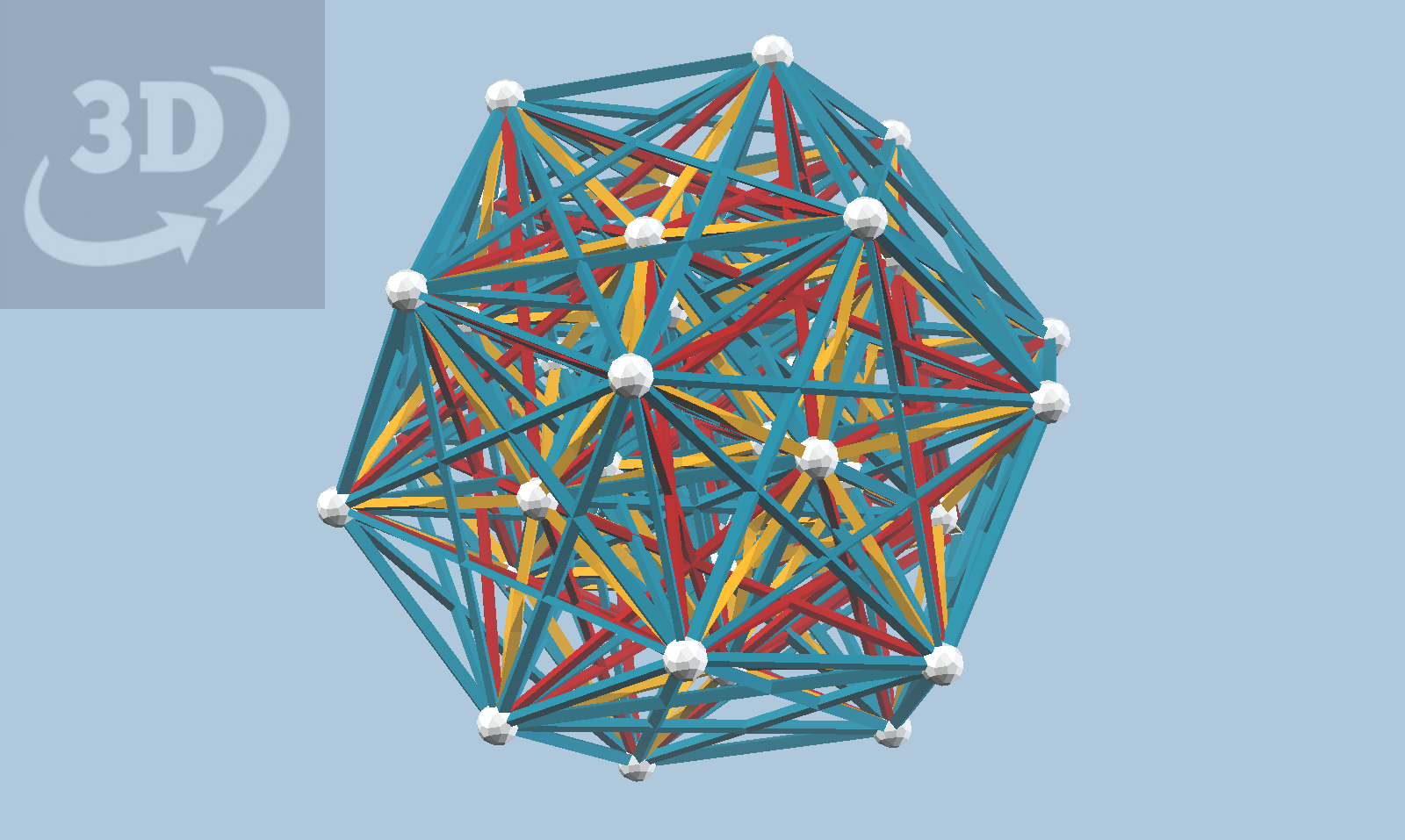
This model is quite a bit less cluttered than the 4_21 projection, but note that there is a high degree of edge intersection near the center. This is made more clear by the beautiful orthogonal projection down a red direction shown below. The model has H_3 symmetry but evidently not H_4, consistent with the fact (?) that E_7 does NOT contain a subgroup isomorphic to H_4. Constructing this in real Zome would be a real challenge!
Now, I've described two separate algorithms using dot products, one to compute the "short" edges given a vertex set, and another to find the vertex figure of a polytope. We can apply these two algorithms to a vertex of 3_21, to produce 2_21, its vertex figure, the Gosset polytope in 6 dimensions. 2_21 has E_6 symmetry. A projection into Zome is shown below. The model has a single axis of fivefold symmetry.
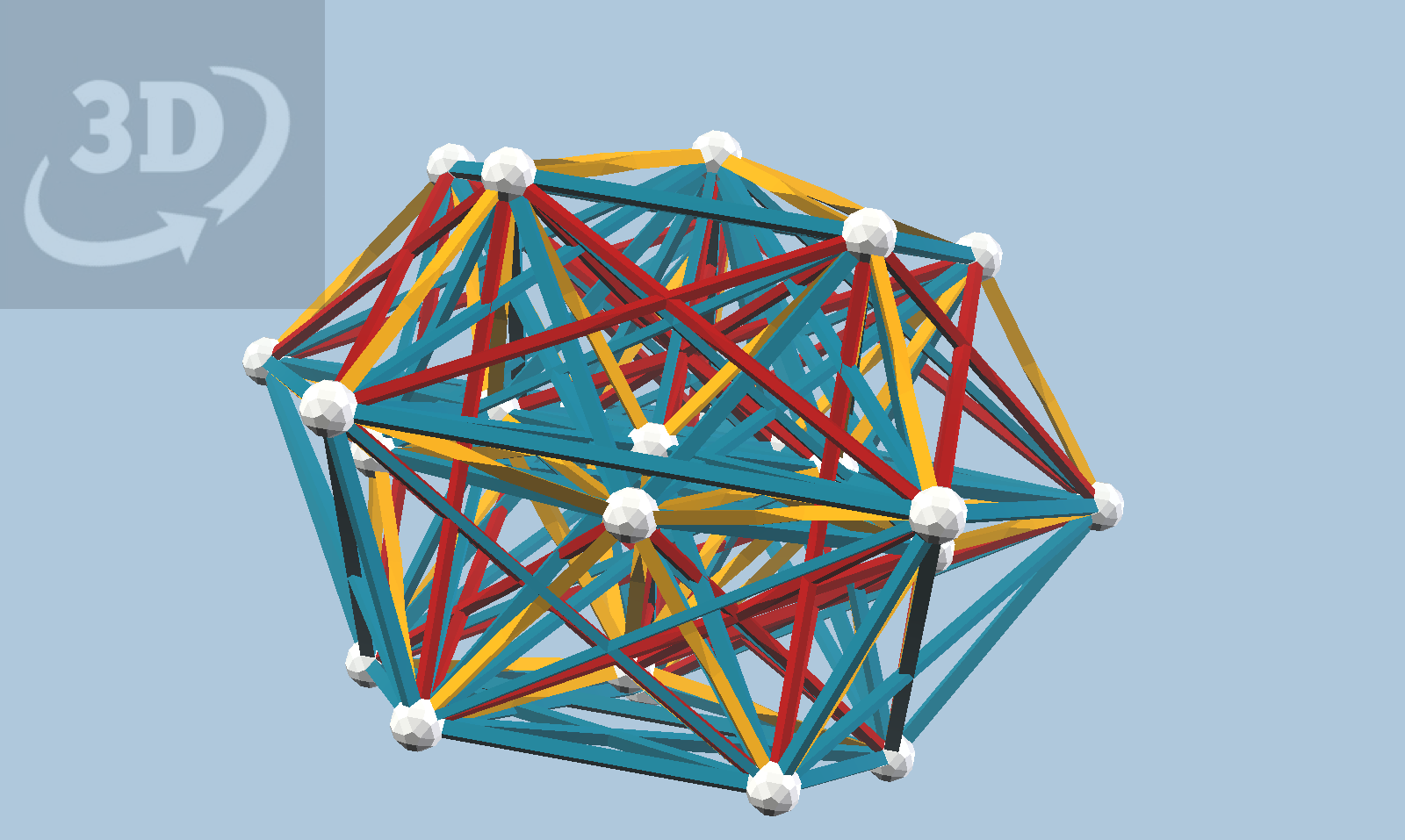
The view below is looking almost directly down the fivefold symmetry axis. This model is very feasible to construct in real Zome, though probably at one "tau scale" larger than shown, to allow for the struts to bypass one another rather than introducing "false vertices" at the intersections.
Do you think these Zome models are complicated? In fact, they are deceptively simple, since such highly symmetric projections of the Gosset polytopes naturally result in a high degree of "coincidence", where separate vertices and edges overlay each other when projected to 3-space. To get a clearer sense of the complexity of these polytopes, one really has to move toward less symmetric projections. Fortunately, vZome offers the ability to perform quaternion rotations on the 4D model before projecting to three dimensions. A "green quaternion" seems to always put the model into a tetrahedral symmetry system, as we saw a couple of weeks ago. Here is such a projection of the 2_21 we just saw:
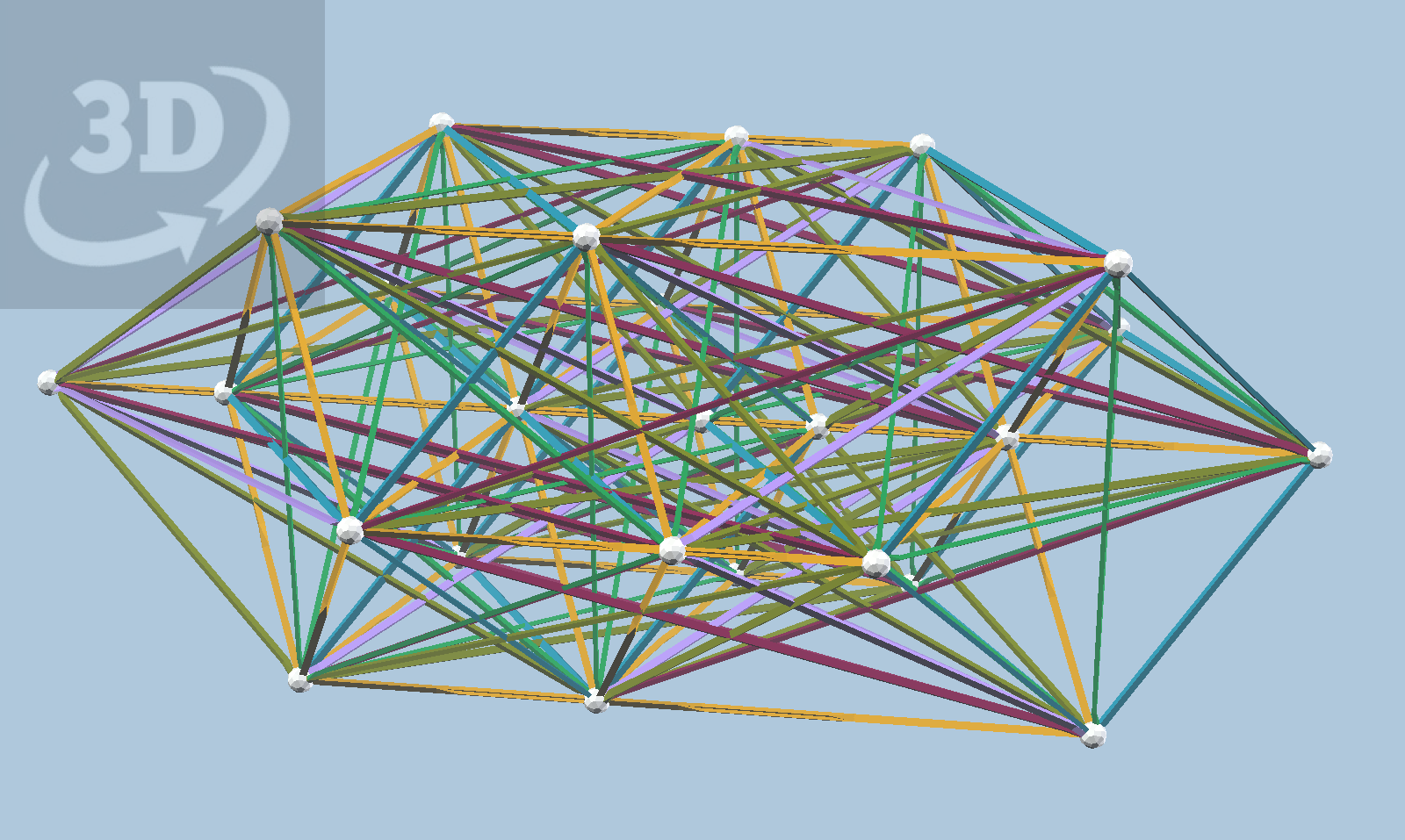
This projection is a model with three-fold symmetry, and the view above shows the model from the side. Note the two corner-wise overlapped blue cubes; these lie along the symmetry axis. Note also the yellow rhombic dodecahedron. The view below shows the model from a viewpoint looking down the symmetry axis. Note how different this projection looks from the "real Zome" projection!
Now, one nice thing about "green quaternion" projection of these models is that it can be done in many different ways! I've tried at least 5 different green directions, and gotten as many very different projections. There may be as many as 30 different projections, although I expect a smaller number like 5 or 12. One can apply the same projections to 3_21 or 4_21, of course. Here is my current favorite "green" projection of 3_21... clearly showing a lot more edges than the icosahedral projection did.
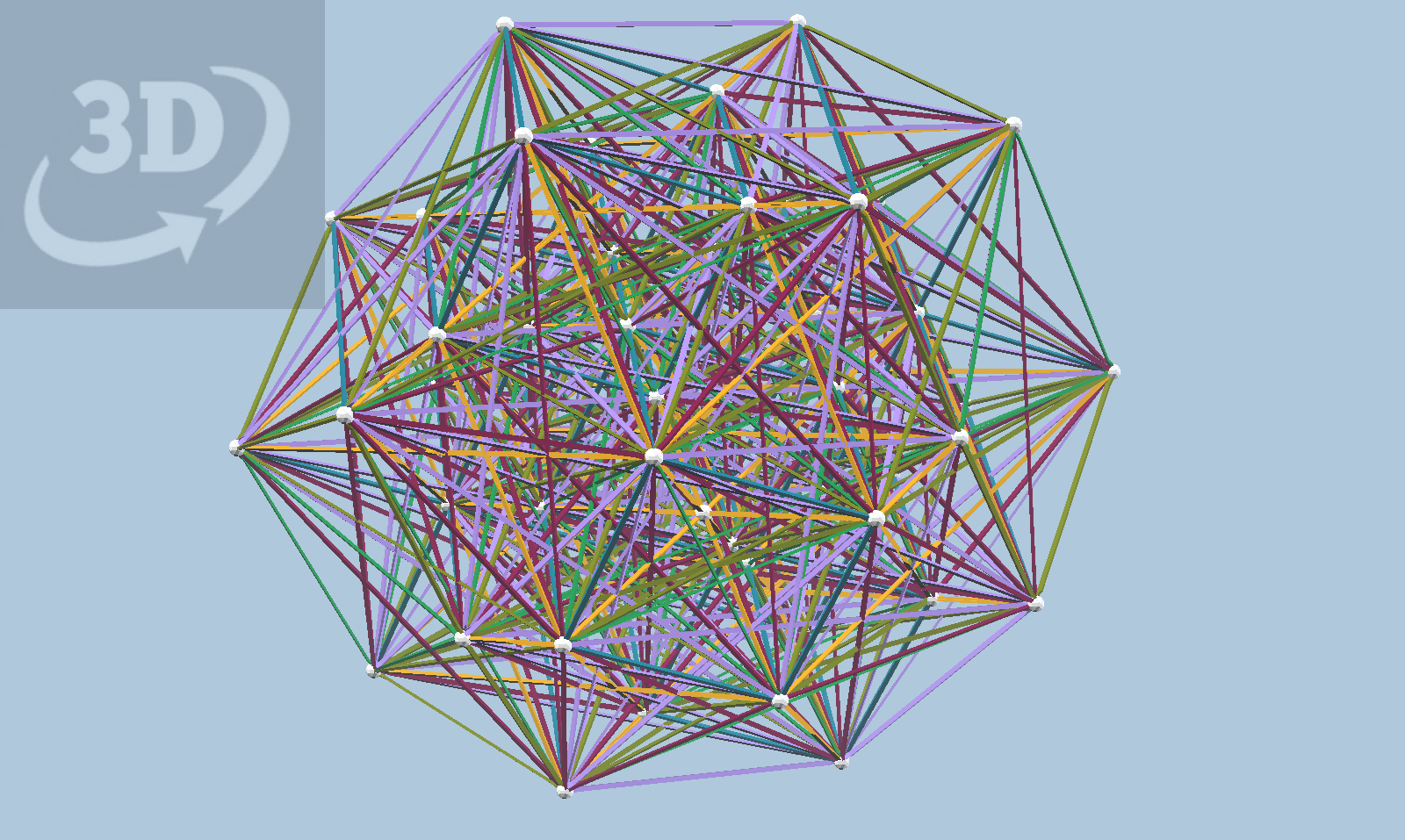
An orthogonal (parallel) projection of this model is shown below; here you can see some hints of five-fold symmetry, in terms of squashed pentagons all over the place.
Naturally, to really get a sense of these projections, you need to turn them over in real time, using vZome. You can also apply your own quaternion rotations before importing the 4D VEF files. For that purpose, you can download the 4_21, 3_21, and 2_21 VEF datafiles to your disk, then use the "import 3D..." vZome command.